Elementary Particle Structure

Introduction 

The Standard model does not have a complete interpretation, the current situation as stated by Jim Baggott¹ is:

 “The theory is not meant to be understood”……. “Today the theory remains a mysterious black top hat from which white rabbits continue to be pulled. Students are advised not to ask how this particular conjuring trick is done”. 

In order to have a theory that is understood we need a formula that explains the basic particle design. A formula that combines mass and radius has been suggested before as summarized in the introduction to a paper by H.J. Fahr and M. Heyl². Numerous Fractional Quantum Hall Experiments have shown the relationship between particles and fractional sequences; added to this the common belief that elementary particles are both wave and particle, then there should be a mathematical formula that explains the relationship between fraction, wavelength, radii and mass. It is proposed that these entities can be linked together by the introduction of a Linear Force Constant.

Before proceeding it is necessary to clarify what is meant by linear force (F_l) and how the Constant Linear force model (CLF) describes the elementary particle.

Currently there are three definitions for mass, CLF reduces this to two by proposing that the elementary particle consists of a vacuum field and an anti-vacuum field; as these are numerically equal and opposite in sign: mass is a measure of the maximum strength of either force or anti-force.

Given that vacuum force is a measurement of the force of empty space, then anti-force is a measurement of something in space. This means that anti-force has density and vacuum force does not have density. It follows that only the something that is the anti-vacuum force carrier; is subject to inertia. The difference in inertia between force and anti-force distorts both fields creating two different waveforms.

As the vacuum force wave is not subject to inertia its wavelength is equal to the field diameter. The inertia of the anti-force wave has to be overcome before it can rotate in harmony with the vacuum force wave. This leads to the anti-vacuum force being subject to acceleration and during the period of acceleration it is wound up within the vacuum wave creating the fractional (electromagnetic) waves observed during Fractional Quantum Hall Effect experiments.

Unless otherwise stated this paper deals with the vacuum wave, it shows the relationship between the Standard model entities and the vacuum wave; it also shows the relationship between de Broglie's wave equation and the CLF particle diameter. The Classical Electron Radius is used as the starting point for the CLF particle diameter and this is justified by showing that the formula is in rough agreement with the radii of both proton and neutron as found by experiment. This means that the particle radii proposed in the CLF model is in agreement with the only three particle radii found by experiment.

It is also show that the mass values predicted using the fractional wave formula are in agreement with the mass values found by experiment; and that the particle diameters predicted using the CLF particle structure equation are the same as the wavelengths predicted by de Broglie's wave equation.

The CLF model connects Einstein's Energy with  Quantum theory (de Broglie's) wave, by using (particle) field structure as an intermediary between Relativity and Quantum theory. It does this by assuming that space and infinity have a continuous particle structure throughout their extent.

The Linear Force Constant

This was found using the known mass and classical electronic radius of the electron

Linear Force equals the Classical Electron Radius times the electron mass:

1.4399648 = 2.817941(fermi) X 0.51099892(MeV)

F_l = rm..…………………………………. (1) 

It will be shown that the diameter of each particle is equal to the vacuum wave length. [The difference between positive and negative charge is not dealt with in this article and the vacuum wave length is that of the +1charge particle, where the F_l constant is equal to the diameter ( ‘2r’ = 2.8799296)]. This can be linked to Einstein's classical formula as follows:

Ec² = m = F_l/2r………….……………….. (2)

Ec² = F_l/2r………………….…………….. (3)

E = energy

c = speed of light

m = mass

F_l = linear force constant (2.8799296)

r = radius

The problem with Einstein's formula is that it gives the energy in the direction of movement (the energy on the compressed lead radial). If the speed is zero then E = m regardless of volume! Einstein does not take into account the difference in density across the diameter of a moving body, but gives a value related to the density on the shortest radial. Removing speed from the equation gives the 'structural' formula in place of the 'moving' or 'collision energy' formula found by Einstein.

The F_l constant is used to find the radii of other particles as shown in table 1 col. (e). Known data for the electron is used to find the linear force constant (F_l). The constant and known mass values are then used to find the radii of  the other particles.

Currently the Standard model does not predict particle radii but, given that all particles have the same charge value; then the classical formula for finding the Classical Electron Radius produces radii for leptons and quarks proportional to those shown in col. (e) of table 1: Indicating that the Standard model practice of allocating fractional charge values to quarks is open to question.

Fractions

Fractional charge⁵ is found in Quantum Hall experiments (TFQHE) and occurs in a number of sequences, The most well known being the so-called ‘fractionally charged electrons’ found by Tsui et al in the sequence 1/3, 2/5, 3/7 etc. (The only other instances of this sequence that I have found are cosmological measurements where this particular fractional sequence refers to the distances between centres of mass).

The fractional sequence for elementary particle compaction is somewhat different, but first a cause is needed to explain why particle compaction (or expansion) occurs in a regular sequence, and wave structure supplies that cause; at the ‘top’ and ‘bottom’ of each wave cycle the wave force has to switch from ‘increasing’ to ‘decreasing’ (or vice versa) and it is suggested that this provides a natural stop point for compaction and expansion. The next stage was to find the fractional sequence that applies to the diameter of particles (the distance between wave peaks and troughs); by mathematical experiment, I found the sequence 1, 1/2, 1/3, 1/4, 1/5 etc. The manner in which this sequence occurs is illustrated in Fig. 1. Table 4 shows the fractions related to  leptons and quarks as given in the 2004 catalogue issued by the Particle Data Group⁶.

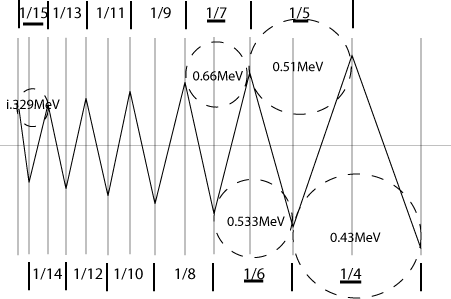
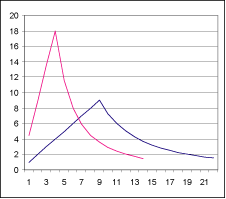
                      Fig.1

Graph of all fractions 1 to 1/1663 and particles

 found by experiment (table 4. Cols. (c) and (d))

Given that the electron is the 1/5 particle, then the fractions for the other particles are as shown in table 4.

Col. (a) is the fraction by which the previous diameter is reduced:

for example, (using the 1/5 diameter to find the 1/6 diameter)    5.635882 - (1/6 x 5.635882)=4.6965684

Col. (b) is the particle diameter.

Col. (c) is the mass found using the Linear Force Constant and the diameter.

Col. (d) is the mass found by experiment³.

Col. (e) is the experimental margin of error.

Col. (f) is the difference between predicted mass (col. c) and the experimental mass (col. d) for comparison with the experimental margin of error.

Col. (g) is the PDG reference.
 

Fig. 2

Graph of particles predicted by fractional wave (black line)

compared with  particles (leptons and quarks, listed in table 4)

 found by experiment (red squares). Note that in this interpretation

 no particles are rejected and the results are not averaged

(as in PDG tables); all experiments are treated as producing

a correct result. (Due to small scale, many of the red squares

 represent more than one particle).

Fractional Quantum Hall Effect

The n,1 fractional sequence (col. 'c' in the table below) is taken from a paper by H.Heiselberg⁶. This is compared with fractions taken from Table 4 of the CLF model. Combining these two columns shows that the same particle is being measured on different axis and in different compaction states; the only change is in the shape of the particle, there is no change in volume; this is the distortion responsible for the alteration of force strength and the creation of the so-called four forces. Fig. 3 shows the table drawn to scale.

Fig. 3

This single plane compaction occurs in FQHE experiments and, naturally, in vortexes; it should not be confused with atomic structure where the action of the electron shells causes spherical (3 dimensional) compaction, causing a change in volume for as long as the compacted particle remains within the atom.

Linear force

Some of the unsolved problems of the Standard model involve the relationship between mass, force and radius, I will only make the point that a mathematical relationship is only possible if there is a uniform relationship between particle structures. But, it goes deeper than that; the Inverse Square Law lies at the root of all the force laws and the cause of this common base, is that all particles have the same quantities, only the volume changes. The different forces are simply the different force relationships between particles of different volume.

Summary

It has been shown how mass values found by experiment are related to classical radii and fractional sequences. It has also been shown that the proposed fractional sequences are related, mathematically, to the fractional sequences found in Fractional Quantum Hall Experiments. This demonstrates that all free particles are distortions of a single elementary particle and that some of the internal quantities of the particle (linear force, and volume) remain unchanged. Given that all particles have the same charge value, the Classical Radius Formula produces the same radii as that found using linear force formula; it is then unlikely that fractional charge values exist in reality and that the charge of the single elementary particle remains unchanged by distortion. This means that infinity consists of particles made up of vacuum fields, and vacuum force carrier, of just one structural design (balanced vacuum fields). The universe is created from particles distorted by vortex action (compacted on one axis only and expanded on the axis at 90 deg. to the compaction axis). A different compaction occurs in atomic structure.

It is proposed that this explains the structure of charged particles in classical terms and lays the foundation for a classical interpretation of particle behaviour.

References 

¹Beyond Measure, Jim Baggott, OUP, 2003 ISBN 0 19 852536 2

² http://arxiv.org/PS_cache/astro-ph/pdf/0606/0606448v2.pdf

³ S. Eidelman et al., Phys. Lett. B 592, 1 (2004) (bibtex)

⁴ http://www.terra.es/personal/gsardin/news13.htm

 ⁵ http://nobelprize.org/nobel_prizes/physics/laureates/1998/press.html

⁶ arXiv:cond-mat/0510688 v2 20 Dec 2005